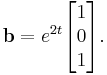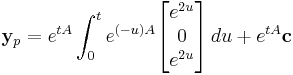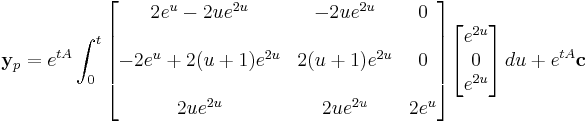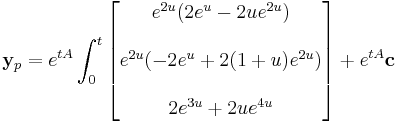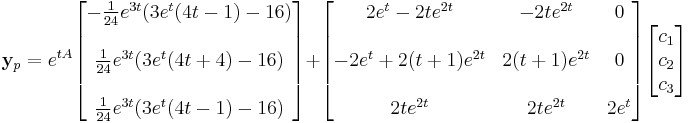Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group.
Let X be an n×n real or complex matrix. The exponential of X, denoted by eX or exp(X), is the n×n matrix given by the power series
The above series always converges, so the exponential of X is well-defined. Note that if X is a 1×1 matrix the matrix exponential of X is a 1×1 matrix consisting of the ordinary exponential of the single element of X.
Contents |
Properties
Let X and Y be n×n complex matrices and let a and b be arbitrary complex numbers. We denote the n×n identity matrix by I and the zero matrix by 0. The matrix exponential satisfies the following properties:
- e0 = I.
- eaXebX = e(a + b)X.
- eXe−X = I.
- If XY = YX then eXeY = eYeX = e(X + Y).
- If Y is invertible then eYXY−1 = YeXY−1.
- exp(XT) = (exp X)T, where XT denotes the transpose of X. It follows that if X is symmetric then eX is also symmetric, and that if X is skew-symmetric then eX is orthogonal.
- exp(X*) = (exp X)*, where X* denotes the conjugate transpose of X. It follows that if X is Hermitian then eX is also Hermitian, and that if X is skew-Hermitian then eX is unitary.
Linear differential equation systems
Main article: matrix differential equation
One of the reasons for the importance of the matrix exponential is that it can be used to solve systems of linear ordinary differential equations. The solution of
where A is a constant matrix, is given by
The matrix exponential can also be used to solve the inhomogeneous equation
See the section on applications below for examples.
There is no closed-form solution for differential equations of the form
where A is not constant, but the Magnus series gives the solution as an infinite sum.
The exponential of sums
We know that the exponential function satisfies ex + y = exey for any real numbers (scalars) x and y. The same goes for commuting matrices: If the matrices X and Y commute (meaning that XY = YX), then
However, if they do not commute, then the above equality does not necessarily hold, in which case we can use the Baker–Campbell–Hausdorff formula to compute eX + Y.
The converse is false: the equation eX + Y = eXeY does not necessarily imply that X and Y commute. However, the converse is true if X and Y contain only algebraic numbers and their size is at least 2×2 (Horn & Johnson 1991, pp. 435–437).
For Hermitian matrices there are two notable theorems related to the trace of matrix exponentials:
Golden–Thompson inequality
If A and H are Hermitian matrices, then
Note that there is no requirement of commutativity. There are counterexamples to show that the Golden–Thompson inequality cannot be extended to three matrices. However, the next theorem accomplishes this in a way.
Lieb's theorem
For a fixed Hermitian matrix  the function
the function
is concave on the cone of positive-definite matrices. [2]
The exponential map
Note that the exponential of a matrix is always an invertible matrix. The inverse matrix of eX is given by e−X. This is analogous to the fact that the exponential of a complex number is always nonzero. The matrix exponential then gives us a map
from the space of all n×n matrices to the general linear group of degree n, i.e. the group of all n×n invertible matrices. In fact, this map is surjective which means that every invertible matrix can be written as the exponential of some other matrix (for this, it is essential to consider the field C of complex numbers and not R).
For any two matrices X and Y, we have
where || · || denotes an arbitrary matrix norm. It follows that the exponential map is continuous and Lipschitz continuous on compact subsets of Mn(C).
The map
defines a smooth curve in the general linear group which passes through the identity element at t = 0. In fact, this gives a one-parameter subgroup of the general linear group since
The derivative of this curve (or tangent vector) at a point t is given by
The derivative at t = 0 is just the matrix X, which is to say that X generates this one-parameter subgroup.
More generally,(R.M. Wilcox 1966)
Taking in above expression 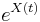 outside the integral sign and expanding the integrand with the help of the Hadamard lemma one can obtain the following useful expression for the derivative of matrix exponent:
outside the integral sign and expanding the integrand with the help of the Hadamard lemma one can obtain the following useful expression for the derivative of matrix exponent:
The determinant of the matrix exponential
It can be shown that for any complex square matrix, the following identity holds:
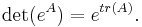
In addition to providing a computational tool, this formula shows that a matrix exponential is always an invertible matrix. This follows from the fact the right hand side of the above equation is always non-zero, and so 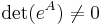 which means that
which means that 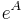 must be invertible. Another observation is the following: in the real-valued case, we see that the map
must be invertible. Another observation is the following: in the real-valued case, we see that the map
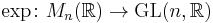
is not surjective (this is in contrast with the complex case mentioned earlier). This follows from the fact that (for real-valued matrices) the right hand side of the above equation is always positive while there exist invertible matrices with a negative determinant.
Computing the matrix exponential
Finding reliable and accurate methods to compute the matrix exponential is difficult, and this is still a topic of considerable current research in mathematics and numerical analysis. Both Matlab and GNU Octave use Padé approximant.[3][4] Several methods are listed below.
Diagonalizable case
If a matrix is diagonal:
then its exponential can be obtained by just exponentiating every entry on the main diagonal:
This also allows one to exponentiate diagonalizable matrices. If 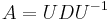 and D is diagonal, then
and D is diagonal, then 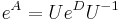 . Application of Sylvester's formula yields the same result.
. Application of Sylvester's formula yields the same result.
Nilpotent case
A matrix N is nilpotent if Nq = 0 for some integer q. In this case, the matrix exponential eN can be computed directly from the series expansion, as the series terminates after a finite number of terms:
Generalization
When the minimal polynomial of a matrix X can be factored into a product of first degree polynomials, it can be expressed as a sum
where
- A is diagonalizable
- N is nilpotent
- A commutes with N (i.e. AN = NA)
This is the Jordan–Chevalley decomposition.
This means that we can compute the exponential of X by reducing to the previous two cases:
Note that we need the commutativity of A and N for the last step to work.
Another (closely related) method if the field is algebraically closed is to work with the Jordan form of X. Suppose that X = PJP −1 where J is the Jordan form of X. Then
Also, since
Therefore, we need only know how to compute the matrix exponential of a Jordan block. But each Jordan block is of the form
where N is a special nilpotent matrix. The matrix exponential of this block is given by
Alternative
If P and Qt are nonzero polynomials in one variable, such that P(A) = 0, and if the meromorphic function
is entire, then
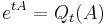 .
.
To prove this, multiply the first of the two above equalities by P(z) and replace z by A.
Such a polynomial Qt can be found as follows. Let a be a root of P, and Qa,t the product of P by the principal part of the Laurent series of f at a. Then the sum St of the Qa,t, where a runs over all the roots of P, can be taken as a particular Qt. All the other Qt will be obtained by adding a multiple of P to St. In particular St is the only Qt whose degree is less than that of P.
Consider the case of a 2-by-2 matrix
The exponential matrix 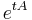 is of the form
is of the form 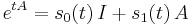 . (For any complex number
. (For any complex number  and any
and any  -algebra
-algebra  we denote again by
we denote again by 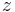 the product of
the product of 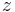 by the unit of
by the unit of  .) Let
.) Let  and
and  be the roots of the characteristic polynomial
be the roots of the characteristic polynomial
Then we have
if 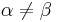 , and
, and
if 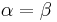 .
.
In either case, writing:
and
where
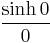 is 0 if t = 0, and 1 if q = 0.
is 0 if t = 0, and 1 if q = 0.
The polynomial 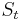 can also be given the following "interpolation" characterization. Put
can also be given the following "interpolation" characterization. Put 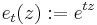 ,
, 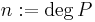 . Then
. Then 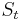 is the unique degree
is the unique degree 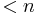 polynomial which satisfies
polynomial which satisfies 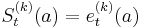 whenever
whenever  is less than the multiplicity of
is less than the multiplicity of  as a root of
as a root of  .
.
We assume (as we obviously can) that  is the minimal polynomial of
is the minimal polynomial of  .
.
We also assume that  is a diagonalizable matrix. In particular, the roots of
is a diagonalizable matrix. In particular, the roots of  are simple, and the "interpolation" characterization tells us that
are simple, and the "interpolation" characterization tells us that 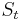 is given by the Lagrange interpolation formula.
is given by the Lagrange interpolation formula.
At the other extreme, if 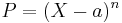 , then
, then
The simplest case not covered by the above observations is when 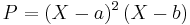 with
with 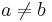 , which gives
, which gives
via Laplace transform
As above we know that the solution to the system linear differential equations given by 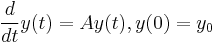 is
is 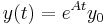 . Using the Laplace transform, letting
. Using the Laplace transform, letting 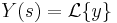 , and applying to the differential equation we get
, and applying to the differential equation we get
where  is the identity matrix. Therefore
is the identity matrix. Therefore 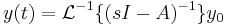 . Thus it can be concluded that
. Thus it can be concluded that 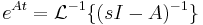 . And from this we can find
. And from this we can find 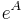 by setting
by setting 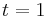 .
.
Calculations
Suppose that we want to compute the exponential of
Its Jordan form is
where the matrix P is given by
Let us first calculate exp(J). We have
The exponential of a 1×1 matrix is just the exponential of the one entry of the matrix, so exp(J1(4)) = [e4]. The exponential of J2(16) can be calculated by the formula exp(λ + N) = eλ exp(N) mentioned above; this yields[5]
+ N) = eλ exp(N) mentioned above; this yields[5]
Therefore, the exponential of the original matrix B is
Applications
Linear differential equations
The matrix exponential has applications to systems of linear differential equations. (See also matrix differential equation.) Recall from earlier in this article that a differential equation of the form
has solution eCty(0). If we consider the vector
we can express a system of coupled linear differential equations as
If we make an ansatz and use an integrating factor of e−At and multiply throughout, we obtain
The second step is possible due to the fact that if AB=BA then 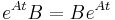 . If we can calculate eAt, then we can obtain the solution to the system.
. If we can calculate eAt, then we can obtain the solution to the system.
Example (homogeneous)
Say we have the system
We have the associated matrix
The matrix exponential
so the general solution of the system is
that is,
Inhomogeneous case – variation of parameters
For the inhomogeneous case, we can use integrating factors (a method akin to variation of parameters). We seek a particular solution of the form yp(t) = exp(tA) z (t) :
For yp to be a solution:
So,
where c is determined by the initial conditions of the problem.
More precisely, consider the equation
with the initial condition 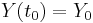 , where
, where
 is an
is an  by
by  complex matrix,
complex matrix,
 is a continuous function from some open interval
is a continuous function from some open interval  to
to 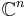 ,
,
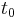 is a point of
is a point of  , and
, and
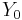 is a vector of
is a vector of 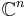 .
.
Left multiplying the above displayed equality by 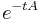 , we get
, we get
We claim that the solution to the equation
with the initial conditions 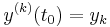 for
for 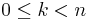 is
is
where the notation is as follows:
![P\in\mathbb{C}[X]](/2012-wikipedia_en_all_nopic_01_2012/I/20f56686c6eaf7e0841ad88aa8362f26.png) is a monic polynomial of degree
is a monic polynomial of degree 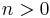 ,
,
 is a continuous complex valued function defined on some open interval
is a continuous complex valued function defined on some open interval  ,
,
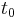 is a point of
is a point of  ,
,
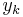 is a complex number, and
is a complex number, and
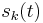 is the coefficient of
is the coefficient of  in the polynomial denoted by
in the polynomial denoted by ![S_t\in\mathbb{C}[X]](/2012-wikipedia_en_all_nopic_01_2012/I/bad75894959eff359dd42def6e3b6f48.png) in Subsection Alternative above.
in Subsection Alternative above.
To justify this claim, we transform our order n scalar equation into an order one vector equation by the usual reduction to a first order system. Our vector equation takes the form
where A is the transpose companion matrix of P. We solve this equation as explained above, computing the matrix exponentials by the observation made in Subsection Alternative above.
In the case 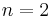 we get the following statement. The solution to
we get the following statement. The solution to
is
where the functions 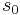 and
and 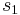 are as in Subsection Alternative above.
are as in Subsection Alternative above.
Example (inhomogeneous)
Say we have the system
So we then have
and
From before, we have the general solution to the homogeneous equation, Since the sum of the homogeneous and particular solutions give the general solution to the inhomogeneous problem, now we only need to find the particular solution (via variation of parameters).
We have, above:
which can be further simplified to get the requisite particular solution determined through variation of parameters.
See also
- Matrix function
- Matrix logarithm
- Exponential function
- Exponential map
- Vector flow
- Golden–Thompson inequality
- Phase-type distribution
- Lie product formula
- Baker–Campbell–Hausdorff formula
References
- ^ Bhatia, R. (1997). Matrix Analysis. Graduate Texts in Mathematics. 169. Springer.
- ^ E.H. Lieb (1973). "Convex trace functions and the Wigner–Yanase–Dyson conjecture". Adv. Math. 11: p. 267–288. H. Epstein (1973). "Remarks on two theorems of E. Lieb". Commun Math. Phys. 31: p. 317–325.
- ^ http://www.mathworks.de/help/techdoc/ref/expm.html
- ^ http://www.network-theory.co.uk/docs/octave3/octave_200.html
- ^ This can be generalized; in general, the exponential of Jn(a) is an upper triangular matrix with ea/0! on the main diagonal, ea/1! on the one above, ea/2! on the next one, and so on.
- Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1.
- Moler, Cleve; Van Loan, Charles F. (2003), "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later", SIAM Review 45 (1): 3–49, doi:10.1137/S00361445024180, ISSN 1095-7200, http://www.cs.cornell.edu/cv/researchpdf/19ways+.pdf.
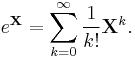
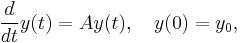
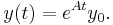
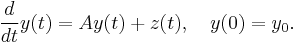
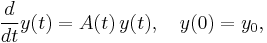
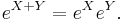
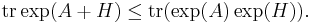
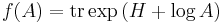
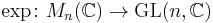
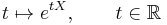
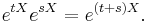
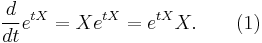
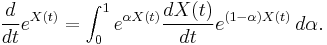
![\left(\frac{d}{dt}e^{X(t)}\right)e^{-X(t)} = \frac{d}{dt}X(t) %2B \frac{1}{2!}[X(t),\frac{d}{dt}X(t)] %2B \frac{1}{3!}[X(t),[X(t),\frac{d}{dt}X(t)]]%2B\cdots](/2012-wikipedia_en_all_nopic_01_2012/I/c2828f71dabd324d2b27bfa8bb89fd31.png)


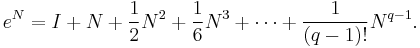
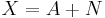
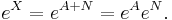
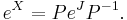
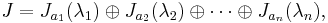
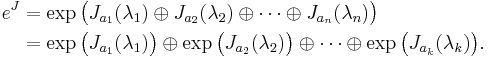
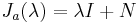
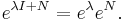
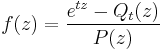
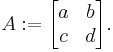
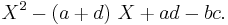
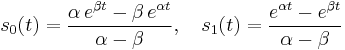
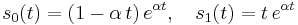
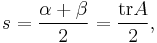
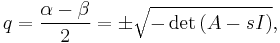
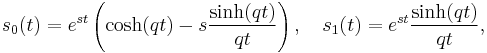
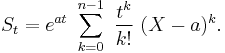
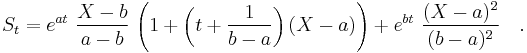
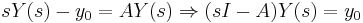
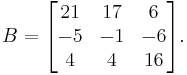
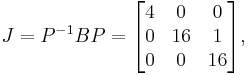
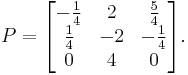
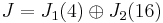
![\begin{align}
\exp \left( \begin{bmatrix} 16 & 1 \\ 0 & 16 \end{bmatrix} \right)
& = e^{16} \exp \left( \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \right) \\[6pt]
& = e^{16} \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} %2B \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} %2B {1 \over 2!}\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} %2B \cdots \right)
= \begin{bmatrix} e^{16} & e^{16} \\ 0 & e^{16} \end{bmatrix}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/e0d7e11df7f5bb619dd71e936b742f0e.png)
![\begin{align}
\exp(B)
& = P \exp(J) P^{-1}
= P \begin{bmatrix} e^4 & 0 & 0 \\ 0 & e^{16} & e^{16} \\ 0 & 0 & e^{16} \end{bmatrix} P^{-1} \\[6pt]
& = {1\over 4} \begin{bmatrix}
13e^{16} - e^4 & 13e^{16} - 5e^4 & 2e^{16} - 2e^4 \\
-9e^{16} %2B e^4 & -9e^{16} %2B 5e^4 & -2e^{16} %2B 2e^4 \\
16e^{16} & 16e^{16} & 4e^{16}
\end{bmatrix}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/afb3346fb3bcee373794ae88c86c1f2f.png)
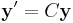
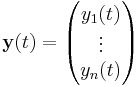
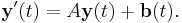
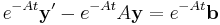
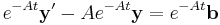
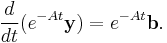
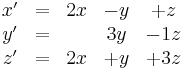
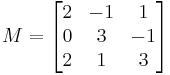
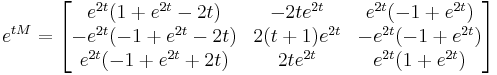
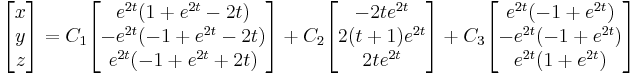
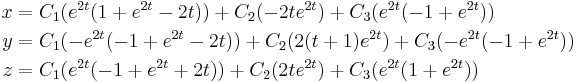
![\begin{align}
\mathbf{y}_p'(t) & = (e^{tA})'\mathbf{z}(t)%2Be^{tA}\mathbf{z}'(t) \\[6pt]
& = Ae^{tA}\mathbf{z}(t)%2Be^{tA}\mathbf{z}'(t) \\[6pt]
& = A\mathbf{y}_p(t)%2Be^{tA}\mathbf{z}'(t).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/58afdc14165d6c825479da895981068c.png)
![\begin{align}
e^{tA}\mathbf{z}'(t) & = \mathbf{b}(t) \\[6pt]
\mathbf{z}'(t) & = (e^{tA})^{-1}\mathbf{b}(t) \\[6pt]
\mathbf{z}(t) & = \int_0^t e^{-uA}\mathbf{b}(u)\,du%2B\mathbf{c}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/9e6baf8415fa2d5addcb112bdcfe0ad8.png)
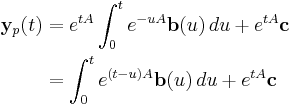
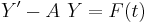
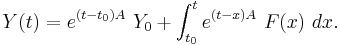
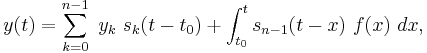
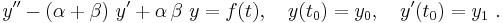
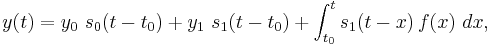
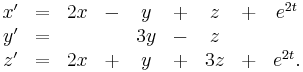
![M= \left[ \begin{array}{rrr}
2 & -1 & 1 \\
0 & 3 & -1 \\
2 & 1 & 3 \end{array} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/cad5fa2307758501472358498469894e.png)